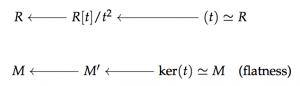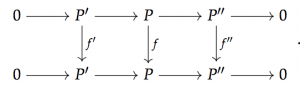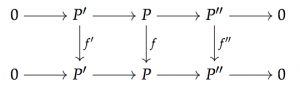Hi all! In this post, I’ll attempt to make some progress towards demystifying the relationship between L-functions and algebraic K-theory, with reference to a very simple example. I’ll say something about L-functions a little lower down, but the only thing I’ll say about K-theory in general is that it’s a way to get a spectrum from, say, a scheme.

The deep connection between these two objects is supposed to be exemplified by the following very approximate and possibly incorrect statement.

Ur-conjecture. [Lichtenbaum, Bloch-Kato, Beilinson, Scholbach…] Let $X$ be a geometric object, probably a scheme of a particular kind, and let $\zeta_X$ be the zeta function associated to $X$. Then for $n$ a sufficiently large positive integer,

$$\zeta_X(n) = \frac {|K_{2n}(X)|_\text{tors}} {|K_{2n - 1}(X)|_\text{tors}} R(n)$$

where $R(n)$ is some factor. Obviously this is completely meaningless until you know what $R(n)$ is, but people do have expressions for it (a relevant buzzword here is “Borel regulator”), about which I’ll say no more. The point is that there are formulae for values of L-functions at integers (and I’m sorry, but I’ll use “L-function” and “zeta function” interchangeably) involving torsion orders of K-groups.

A conjecture of this form has been proven for $X$ the ring of integers of a totally real abelian field by piling Iwasawa theory and other manoeuverings onto the cases of the Quillen-Lichtenbaum conjecture proven by Voevodsky. It’s a humongous proof. In general, these conjectures are wide open and should be regarded with reverence.

L-functions

Before I really get going, though, I’m going to say a word about L-functions, which by convention are meromorphic functions on $\mathbb{C}$ with certain properties. I’m going to list these salient properties in bnew, and illustrate them using the historically first L-function, which is of course the Riemann zeta $\zeta(s)$. We’ll later find that each of these properties has a purely homotopy-theoretic analogue on the K-theory spectrum.

Dirichlet series. To an L-function $L$ is associated a Dirichlet series expansion

$$\sum_{n \geq 0} a_n n^{-s}.$$

with $a_n \in \mathbb{C}$. $\zeta(s)$ has $a_n = 1$ for all $n$.

Abscissa of convergence. There is some $\sigma \in \mathbb{R}$, called the abscissa of convergence, such that the Dirichlet series converges to $L(s)$ for $\mathbf{Re}(s) > \sigma$. The abscissa of convergence of $\zeta$ is 1.

Euler product expansion. There is an infinite product, typically over closed points of a scheme, of nice simple functions that also converges to $L(s)$ on some respectable proportion of $\mathbb{C}$. The Euler product expansion of $\zeta$ is

$$\prod_{p \text{ prime}} \frac 1 {1 - p^s}.$$

Analytic continuation. This is implicit in the fact that I said an L-function was a meromorphic function on $\mathbb{C}$ in the first place, but if you take the more practical view that an L-function is defined by its Dirichlet series or Euler product, there’s some content here, and analytic continuation statements are usually hard to prove.

Functional equation. An L-function has a (possibly twisted) reflective symmetry: there is some real number $\tau$, frequently equal to the abscissa of convergence, such that

$$L(s) = A(s) L(\tau - s).$$

For the Riemann zeta, we have (lifted from Wikipedia) $\tau = 1$ and

$$A(s) = 2^s \pi^{s-1} \sin \left (\frac {\pi s} 2 \right) \Gamma(1 - s)$$

This just comes from the Archimedean L-factor (we’ll say nothing about that here) but there can be other things too. Analytic continuation and functional equation are usually proved together.

You probably expect to be able to formulate a Riemann hypothesis for a general L-function, too, but we won’t get into that here.

The simplest L-function

I said the Riemann zeta was the historically first L-function, but it’s not the simplest. The simplest is the zeta function of a finite field $\mathbb{F}_q$, which is a single Euler factor:

$$\Xi_q(s) = \frac 1 {1 - q^s}.$$

The number theorists probably use different notation for this, but I am a carefree rogue who does as he wills.

$\Xi_q$ is manifestly meromorphic; it is its own Euler product; its Dirichlet series is given by expanding the above expression as a geometric series, with abscissa of convergence $0$; and its functional equation is

$$\Xi_q(-s) = -q^s \Xi_q(s).$$

This is the only example of an L-function which one can comfortably manipulate with one’s hands without substantial analytic ingenuity. It’s this basic example that we’ll spend much of the rest of this blog post studying.

The K-theory of a finite field

In a 1972 paper, Quillen proved one of my all-time favourite theorems by describing the homotopy type of the K-theory spectrum of a finite field.

Theorem. [Quillen] The connected component $K(\mathbb{F}_q)_0$ of the $0$-space of the K-theory spectrum of $\mathbb{F}_q$ fits into a fibre sequence

$$K(\mathbb{F}_q)_0 \to BU \overset{\psi^q - 1} \to BU.$$

where $\psi^q$ is the $q$th Adams operation.

This is the only example of a (global) K-theory spectrum which one can comfortably manipulate with one’s hands without substantial topological ingenuity. By Bott periodicity, we know the homotopy groups of BU:

$$\pi_n BU = \begin{cases} \mathbb{Z} & n = 2m > 0 \text{ is even;} \\ 0 & \text{otherwise.} \end{cases}$$

We also know that $\psi^q$ acts by multiplication by $q^m$ on $\pi_{2m} BU$. That means we can read off the positive-degree homotopy groups of $K(\mathbb{F}_q)$:

$$K_n (\mathbb{F}_q) = \begin{cases} \mathbb{Z}/(q^m - 1) & n = 2m - 1 \text{ is odd;} \\ 0 & \text{otherwise.} \end{cases}$$

Motivated by the ur-conjecture stated above, let’s define a function $f_q : \mathbb{N} \to \mathbb{C}$ by

$$f_q(n) = \frac {|K_{2n}(\mathbb{F}_q)|} {|K_{2n - 1}(\mathbb{F}_q)|}.$$

Suppose, as if possessed by a ghost, you wrote this function down without ever having heard of an L-function. You would still notice that

$$f_q(n) = \frac 1 {q^n - 1}$$

is the restriction to $\mathbb{N}$ of an obvious complex-analytic function: $-\Xi_q$. This is the easiest case of the conjecture.

Now what of the values of $\Xi_q$ at negative integers? We might hope that they have something to do with the negative homotopy groups of $K(\mathbb{F}_q)$, which is, after all, a spectrum. But as things stand, these negative homotopy groups are zero. This rift is signaling that the arithmetic incarnation of the bare K-theory spectrum is not the L-function; rather, it’s the Dirichlet series of the L-function, or the part of the L-function to the right of the abscissa of convergence. The topological object that we should really associate to the full L-function is the K(1)-localisation of the K-theory spectrum. To do this, we need to fix an ambient prime $p$, and let’s make sure it’s different from the characteristic of $\mathbb{F}_q$.

The K(1)-localisation of the K-theory of a finite field

I’m going to self-consciously write out all $L_{K(1)}$s in full. It’ll take up space, but hopefully it’ll aid clarity of notation.

Here’s a slight variant of Quillen’s calculation; if you like, it arises by applying the Bousfield-Kuhn functor to the statement of Quillen’s theorem above.

Proposition. The K(1)-localised K-theory spectrum $L_{K(1)} K(\mathbb{F}_q)$ fits into a fibre sequence

$$L_{K(1)} K(\mathbb{F}_q) \to KU^\wedge_p \overset{\psi^q -1} \to KU^\wedge_p.$$

Thus the homotopy groups of $L_{K(1)} K(\mathbb{F}_q)$, positive and negative, are given by

$$\pi_n L_{K(1)} K(\mathbb{F}_q) = \begin{cases} \mathbb{Z}_p / (q^m - 1) & n = 2m -1 \text{ odd}\\ \mathbb{Z}_p & n = 0 \\ 0 & \text{otherwise.} \end{cases}$$

Until further notice, when we talk about the “value” of an L-function at a point, we’ll mean up to multiplication by a rational number which is a p-adic unit. With this caveat, we now have the identity

$$\Xi_q(n) = \frac {|\pi_{2n} L_{K(1)} K(\mathbb{F}_q)|} {|\pi_{2n - 1} L_{K(1)} K(\mathbb{F}_q)|}$$

for all $n \in \mathbb{Z}$, except at $n = 0$, where things are untidy because $\Xi_q$ has a pole and both homotopy groups in the formula are infinite, and a regulator gets involved. That’s nice.

We need to make a couple more observations about the homotopy groups of the localised K-theory spectrum.

First, the natural map

$$K(\mathbb{F}_q)^\wedge_p \to L_{K(1)} K(\mathbb{F}_q)$$

is an equivalence in degrees greater than $0$. (It’s also an equivalence in degree $0$, but I’d like to propose that we regard that as an accident.) This $0$ is the very same $0$ that occurs as the abscissa of convergence of $\Xi_q$, and it also shows up as the étale cohomological dimension of $\mathbb{F}_q$ minus 1 - a number I’d like to refer to as the Quillen-Lichtenbaum constant of $\mathbb{F}_q$.

Second, the functional equation for $\Xi_q(n)$ is reflected in the homotopy groups of $L_{K(1)} K(\mathbb{F}_q)$ as follows. For any integer $m$, the $p$-adic valuation of $q^m - 1$ is the same as that of $q^{-m} - 1$. Thus for any odd integer $n$, we have an isomorphism

$$\pi_n L_{K(1)} K(\mathbb{F}_q) \cong \pi_{-2 - n} L_{K(1)} K(\mathbb{F}_q).$$

Can this apparent duality be given a topological explanation?

Gross-Hopkins and Spanier-Whitehead duality

We’re going to do this by invoking a total of four or five different dualities, one of which is deep and will be totally blackboxed, so get ready.

Let’s start tackling this by rearranging the above isomorphism slightly. Both of the groups there arise as quotients of $\mathbb{Z}_p$, so they come with a choice of generator: the image of $1$. That means that either group can be identified with its Pontryagin dual, so let’s do it on the left:

$$(\pi_n L_{K(1)} K(\mathbb{F}_q))^\vee \cong \pi_{-2 - n} L_{K(1)} K(\mathbb{F}_q).$$

There, now it looks more like a sensible duality. And the Pontryagin dual in there is a strong hint that Brown-Comenetz duality is involved. Briefly, the Brown-Comenetz dualising spectrum is a spectrum $I$ defined by the natural isomorphism

$$\pi_n \mathbf{Map}(E, I) \cong (\pi_{-n} E)^\vee$$

for spectra $E$. To save pixels, we’ll write $IE$ for $\mathbf{Map}(E, I)$. Now our isomorphism reads

$$\pi_{-n} I(L_{K(1)} K(\mathbb{F}_q)) \cong \pi_{-2-n} L_{K(1)} K(\mathbb{F}_q).$$

But height 1 Gross-Hopkins duality states that for a K(1)-local spectrum E,

$$IME \cong \mathbf{Map}(E, L_{K(1)} \mathbb{S}^{-2}).$$

Here $M$ is the first monochromatic slice functor, which for a K(1)-local spectrum is just the fibre of the map to its rationalisation. $M$ isn’t doing anything too destructive here, so let’s omit it for now and figure out its role in a moment. We’ve arrived at

$$\pi_{-2-n} \mathbf{Map}(L_{K(1)} K(\mathbb{F}_q), L_{K(1)} \mathbb{S}) \cong \pi_{-2-n} L_{K(1)} K(\mathbb{F}_q).$$

at least for odd $n \neq -1$. So we’d be home if $K(\mathbb{F}_q)$ were to be K(1)-locally Spanier-Whitehead self-dual. And it is! I learned this in Dustin Clausen’s thesis defence, but one can prove it by showing that

$$KU^\wedge_p \wedge KU^\wedge_p \overset{\mu} \to KU^\wedge_p \overset{J} \to L_{K(1)} \mathbb{S}^{-1}$$

exhibits $KU^\wedge_p$ as K(1)-locally self-dual up to a shift of 1, compatibly with Adams operations, and plugging this into the fiber sequence for $L_{K(1)}K(\mathbb{F}_q)$. And thus the duality is explained.

Let’s circle back for a moment and say a quick word about the role of the monochromatic slice functor $M$. Since $L_{K(1)} K(\mathbb{F}_q)$ doesn’t have many torsion-free homotopy groups, the only effect of $M$ is to convert the $\mathbb{Z}_p$s in degrees $0$ and $-1$ into $\mathbb{Q}_p/ \mathbb{Z}_p$s in degrees $-1$ and $-2$. But that was exactly what was needed to get the original duality statement to work in those degrees, once we put in the Pontryagin dual. Thus the duality is not merely explained but embellished with a pristine little bow.

The dictionary, and some questions

As promised, we’ve given homotopy-theoretic interpretations of (almost) all the fundamental analytic properties of L-functions. Here’s a table to summarise:

Analysis		Topology
L-function		K(1)-localised K-theory spectrum
Dirichlet series		Bare K-theory spectrum
Abscissa of convergence		Quillen-Lichtenbaum constant
Euler product		?? (But see below)
Analytic continuation		K(1)-localisation
Functional equation		Gross-Hopkins + Spanier-Whitehead duality

(I apologise for the poor formatting - I’m not used to Markdown, and the latex support doesn’t seem to run to table environments).

Some questions I don’t know how to answer at this point:

• Let X be a Dedekind domain, L its field of fractions, and $k(x)$ the residue field at a closed point $x \in X$. Then there’s a cofiber sequence

$$\bigvee_{x \in X} K(k(x)) \to K(X) \to K(L)$$

The left-hand arrow looks an awful lot like it’s trying to express K(X) as an Euler product over x of K(k(x)), but I don’t know how to make that precise. K(L) is a nuisance.

• Now let X be a smooth proper variety over $\mathbb{F}_q$. There’s a spectral sequence with $E_2$ term given by étale cohomology of X with suitably Tate-twisted $\mathbb{Z}_p$ coefficients which abuts to the K(1)-local K-theory of X. Can we use this to relate the formula for the zeta function of X in terms of the characteristic polynomial of Frobenius on étale cohomology to a K-theoretic description of the special values?

• What’s the analogue of $K(\mathbb{F}_q)$ for an archimedean L-factor? This might be related to work of Connes and Consani on cyclic homology with adelic coefficients.

p-adic L-functions

This section is tangential to the rest of the post, but I think it suggests some interesting avenues of investigation. Up until now we’ve been discussing L-functions defined on $\mathbb{C}$, but L-functions defined on $\mathbb{Z}_p$ are also of interest to number theorists. We’ll construct the p-adic analogue of an Euler factor, and see that it throws up some unexpected topology.

In this section, we’ll assume that $p$ is odd. Things are probably substantially more awkward when $p = 2$.

Let’s return (up to sign) to our function $f_q$, this time regarded as a function $\mathbb{N} \to \mathbb{Q}_p$:

$$f_q(n) = \frac 1 {1 - q^n}.$$

We’d like to extend $f_q$ to a continuous function $E_q: \mathbb{Z}_p \to \mathbb{Q}_p$. p-adic continuity sounds weak compared to complex analyticity, but it’s actually kind of hard to be p-adically continuous, and since $\mathbb{N}$ is dense in $\mathbb{Z}_p$, we’re going to have at most one choice of extension.

In fact, we don’t have any choices, a fact which won’t surprise anyone who’s studied p-adic L-functions before. The proof of this is a byproduct of the construction of the real p-adic L-function. Let

$$S = \{n \in \mathbb{N} \, | \, q^n \equiv 1 \mod p.\}$$

Observe that $S$ is already dense in $\mathbb{Z}_p$, so if we can find a continuous function $\mathbb{Z}_p \to \mathbb{Q}_p$ that agrees with $f_q$ on $S$, that’s the best we can do, whether the two functions agree on the whole of $\mathbb{N}$ or not.

Here’s the crux: There’s a continuous function

$$\log : \mathbb{Z}_p \to p\mathbb{Z}_p$$

known as the Iwasawa logarithm, and a continuous function

$$\exp: p\mathbb{Z}_p \to \mathbb{Z}_p$$

known as the p-adic exponential. They have most of the properties you’d expect of a pair of functions called $\exp$ and $\log$, except that the identity

$$\exp (\log (x)) = x$$

only hnews when $x$ is congruent to $1$ mod $p$. In general,

$$\exp (\log(x)) = p^r \omega x$$

where the integer $r$ and the $(p-1)$st root of unity $\omega$ are uniquely determined by the requirement that $p^r \omega x \equiv 1 \mod p$.

So we can follow our hearts and define

$$E_q(s) = \frac 1 {1 - \exp(s \log q)}$$

but we have to live with the fact that $E_q(n) = f_q(n)$ only when $n \in S$. For general $n \in \mathbb{N}$,

$$E_q(n) = \frac 1 {1 - (\omega q)^n}$$

for a suitable $(p-1)$st root of unity $\omega$.

Fine. Where’s the topology? What spectrum is $E_q$ telling us about? At integers outside $S$, the values of $E_q$ don’t match up with the homotopy groups of $L_{K(1)} K(\mathbb{F}_q)$ anymore. Instead,

$$E_q(n) = \frac {|\pi_{2n} M|}{|\pi_{2n - 1} M|}$$

for all integers $n \neq 0$, where M is a K(1)-local spectrum defined as the fiber of

$\psi^{\omega q} - 1 : KU^\wedge_p \to KU^\wedge_p$.

So, a couple more questions:

• What’s special about M? Why is it any better than $L_{K(1)}K(\mathbb{F}_q)$? What other spectra are “p-adically continuous” in this sense?

• Constructing p-adic L-functions more serious than $E_q$ usually requires some fairly heavy p-adic analysis. Can we partly bypass this by proving p-adic continuity results for the Picard-graded homotopy groups of certain K(1)-local spectra and using the orders of these homotopy groups? I believe some such continuity results already exist, in the folklore if not in the literature.

Thanks for reading this many words! Let me finish up by remarking that some of the stuff in this post carries through to K-theory spectra of rings of integers, and using work of Dwyer and Mitchell as a bridge, one can obtain results on the special values of Kubota-Leopnewt-type p-adic zeta functions. If I can think of enough interesting stuff to say about that, it might be the subject of a future post.

I think the Chromotopy platform doesn’t currently support blog comments, but if you have any comments or questons, please email me at sglasman at math dot mit dot edu.

---

Update: Dustin Clausen emailed me with some helpful comments about the Spanier-Whitehead self-duality of $L_{K(1)} K(\mathbb{F}_q)$, resulting in some alterations in the text.

For the purposes of this post, I am going to assume that you are all familiar with the basics of Algebraic $K$-theory. If you’re not, just treat it as a black box, a gadget which takes in one of :

• a (simplicial) ring (spectrum)
• an augmented (simplicial) bimodule over a ring
• an exact category
• a Waldhausen category
• a small, stable $\infty$-category

and spits out a spectrum $K(\mathcal{C})$, such that $K(\mathcal{C})$ does the job of  ”storing all Euler characteristics” or “additive invariants”.

An important example is when $\mathcal{C}$ is the category of finitely generated projective modules over a ring $R$, and then we call this $K(R)$. It is a generally-accepted fact that the $K$-theory of rings is generically a very difficult and often useful thing to compute (knowledge of the $K$-groups of $\mathbb{Z}$, for example, would be quite valuable to many). In an ideal world, we would be able to understand the functor

$$A \mapsto \tilde{K}(A) = hofib(K(A) \rightarrow K(R))$$

on the category of algebras augmented over a given ring $R$, but this ends up being fairly intractable. One might hope that it would be easier to look at what happens when restricted to free augmented algebras, that is looking at the functor on (flat) $R$-bimodules

$$M \mapsto \tilde{K}(T_R (M)),$$

where $T_R (M)$ is the tensor algebra on $M$. This is pretty tough, but it turns out that we can do it. Let’s take a baby step first, and try to understand the K-theory of the “linearized” tensor algebra. The 1st Goodwillie derivative of the identity functor on augmented $R$-algebras is given by

$$P_1 (id) (A) = A / I^2 ,$$

where $I$ is the augmentation ideal of $A$. In the case where $A = T_R (M)$ for some $R$-bimodule $M$, then the Goodwillie derivative $P_1 (id)(T_R (M)) = R \oplus M$, where $R \oplus M$ is the the square-zero extension of $R$ by $M$, the ring given by demanding that $M^2 = 0$. In studying the $K$-theory of square-zero extensions, then, we are also studying the $K$-theory of the linearization of the tensor algebra functor (note how many simplifications we have already done!).

A different strategy for dealing with this computational difficulty is to try and understand how the $K$-theory of a ring changes as we “perturb” the ring. To do this, we look at “parametrized $K$-theory” (or the “$K$-theory of parametrized endomorphisms”):

Definition. Let $R$ be a ring, and let $M$ be an $R$-bimodule. We define the parametrized $K$-theory of $R$ with coefficients in $M$, $K(R;M)$, to be the $K$-theory of the exact category of pairs $(P,f)$ where $P$ is a finitely-generated projective $R$-module and $f: P \rightarrow P \otimes_{R} M$ is a map of $R$-modules.

We think about $K(R;M)$ as being the $K$-theory of endomorphisms with coefficients that are allowed to be in $M$. If our picture of a finitely-generated projective $R$-module $P$ is as living as a summand of a rank $n$ free $R$-module, then an element of the above exact category is an $n \times n$ matrix with entries in $M$ that commutes with the projection map $R^n \rightarrow R^n$ defining $P$.

Why should we look towards endomorphisms as perturbations? Well, the picture is supposed to be the following: Let $R$ be a ring and $M$ an $R$-bimodule. This is the same data as a sheaf $\mathcal{F}_M$ over $\operatorname{Spec}(R)$, and we would like to think of a deformation of this over, say, $R[t]/t^2$ as a flat sheaf $\mathcal{F}_{M'}$ over $R[t]/t^2$ (a module) that restricts to $\mathcal{F}_M$ over $\operatorname{Spec}(R)$.

which corresponds to an element of $\operatorname{Ext}^1_R (M,M)$, or a derived endomorphism. The idea is that an extension of $M$ corresponds to a deformation of $M$, which is a reasonable perspective.

The above definition is not immediately seen to be relevant to our original stated desire to study perturbations, but in the investigations of Dundas and McCarthy of stable $K$-theory, the $K$-theory of endomorphisms naturally comes up. In this paper they prove the following theorem:

Theorem. For $R$ a ring and $M$ a discrete $R$-bimodule)

$$\tilde{K}(R;B_\bullet M) \simeq \text{hofib} \left\{ K(R \oplus M) \rightarrow K(R) \right\} = \tilde{K}(R \oplus M),$$

where $R \oplus M$ is again the the square-zero extension of $R$ by $M$.

We think of $R \oplus M$ as a perturbation of $R$ by $M$, as the elements that we are adding on (those coming from the direct summand $M$) are “so small’’ that they multiply to zero. This result relates the “perturbation’’ approach to understanding $K$-theory to our earlier potential approach of understanding the free objects in the category of augmented $R$-algebras.

That’s great, but we’d like to actually have some idea of what these things are. To get a hint at what we should be looking for, we go back to what was classically studied by Almkvist et al.

$K$-Theory of Endomorphisms: The Classical Story

Definition. Let $R$ be a ring and consider the category $End(R)$, whose objects are pairs $(P,f)$ with $P$ a finitely-generated projective $R$-module and $f:P \rightarrow P$ an endomorphism. The morphisms in this category are commutative diagrams of the appropriate type.

Now, we might ask what possible “additive invariants’’ there are on this category, having in mind a few examples. The key (and, as it turns out, universal) one is the following:

Example. [The Characteristic Polynomial] Let $(P,f) \in End(R)$, then the characteristic polynomial of $f$ is given by

$$\lambda_t (f) = \sum_{i \geq 0} Tr(\Lambda^i f)t^i.$$

This can also be obtained in the usual way as a determinant.

The important property of the characteristic polynomial is that if we have a commutative diagram in $End(R)$

with exact rows, then

$$\lambda_t (f) = \lambda_t (f') \cdot \lambda_t (f''),$$

meaning that the characteristic polynomial takes short exact sequences of endomorphisms to products (which are sums in the abelian group where the characteristic polynomials lie).

We now know that a search for additive invariants is a desire to compute $K$-theory, and so we define:

Definition. $K_0 (End(R))$ is defined to be the free abelian group on isomorphism classes of objects in $End(R)$ modulo the subgroup generated by the relations $[(P,f)] = [(P',f')] + [(P'',f'')]$ if there is a commutative diagram

with the rows exact. There is a natural splitting

$$K_0 (End(R)) \simeq K_0 (R) \times \tilde{K}_0 (End(R))$$

coming from thinking of the category of finitely generated projective $R$-modules as living in $End(R)$ as the guys with $0$ endomorphisms.

Of course, $End(R)$ is an exact category, and we could define higher $K$-groups for this as well.

$K_0 (End(R))$ is the repository for additive invariants, in that it has the following universal property:

Proposition. Let $F$ be a map from the commutative monoid of isomorphism classes of objects in $End(R)$ to an abelian group $A$, such that $F$ splits short exact sequences as above. Then $F$ factors through $K_0 (End(R))$, or $K_0(End(R))$ is the initial abelian group for which short exact sequences of endomorphisms split.

What does this look like, though? Well, let’s go back to the characteristc polynomial:

Theorem. The map

$$c: [(P,f)] \mapsto ([P], \lambda_t (f))$$

is an isomorphism

$$K_0 (End(R)) \simeq K_0 (A) \times \tilde{W}(R),$$

where

$$\tilde{W} (R) = \left \{ \dfrac{1 + a_1 t + \dots + a_n t^n}{1+ b_1t + \dots + b_m t^m} ; \; a_i, b_j \in R \right \}$$

is the multiplicative group of fractions with constant term 1.

The moral of this is that the characteristic polynomial encodes all of the additive information about an endomorphism (the trace is a special case of this, of course, being read off by the constant term of the characteristic polynomial). Something interesting is the following:

Proposition. The inclusion $\tilde{W}(R) \rightarrow W(R)$ exhibits $\tilde{K}_0 (R)$ as a dense $\lambda$-subring of $W(R)$, where $W(R)$ are the big Witt vectors of $R$, modelled as power series with constant term $1$.

This means that we might as well think of the big Witt vectors as being limits of characteristic polynomials of endomorphisms, which is the starting point for the line of thought that led to the Lindenstrauss and McCarthy results.

It is also important to mention what some of the uses of this equivalence are:

• Calculations that may be difficult to perform on Witt vectors might be easy if we think of them as coming from characteristic polynomials of endomorphisms;
• Operations that exist on Witt vectors get turned into operations on K-theory, and vice-versa:
• The $n$-th ghost map is given by $gh_n ([P,f] = tr(f^n))$;
• The Frobenius map is given by $F_n ([P,f]) = [P, f^n]$;
• The Verschiebung map is given by $[V_n ([P,f]) = [P^{\oplus n}, v_n f]$, where $v_n f$ is represented by a shift in the first $n-1$ factors and action by $f$ in the last factor. This represents an $n$-th root of $f$, in that $V_n^n$ looks like applying $f$ to all of the blocks of $P^{\oplus n}$.

Lindenstrauss-McCarthy and Topological Witt Vectors

The first thing to do to start generalizing the previous construction is to allow for a “parametrization’’, like we said before.

Definition. Let $R$ be a ring and $M$ an $R$-bimodule. $End(R;M)$ is the category whose objects are pairs $(P,f)$ with $P$ a finitely generated projective $R$-module and $f: P \rightarrow P \otimes_R M$ a map of $R$-modules. As in $End(R)$, morphisms are commutative diagrams.

$End(R;M)$ inherits an exact/Waldhausen structure from considering what’s happening in the “base’’, and so it makes sense to define parametrized $K$-theory as

$$K(R;M) := K(End(R;M)).$$

There is a natural map from $End(R;M)$ to the category of finitely generated projective $R$-modules that forgets the endomorphism, and so we can reduce and consider

$$\tilde{K}(R;M) := hofib(K(R;M) \rightarrow K(R)).$$

We can also consider $M$ to be simplicial by geometrically realizing, and this assembles to a functor

$$\tilde{K}(R;-): \left\{\text{simplicial } R\text{-bimodules} \right \}\; \rightarrow \text{Spectra},$$

which is a good setting to do Goodwillie calculus.

The remarkable result of Lindenstrauss-McCarthy is the following:

Theorem. The functors $\tilde{K} (R; -), W(R;-)$ from simplicial $R$-bimodules to spectra have the same Taylor tower, where $W(R;-)$ is a “topological Witt vectors’’ construction.

Now, this is only remarkable if I tell you what this $W(R;-)$ functor is, so let’s do that. Lindenstrauss and McCarthy describe this using the (notationally cumbersome) language of FSPs instead of spectra or spectral categories, which makes everything a bit hard to read. The idea is a bit simpler, however.

Construction. Let $R$ be a ring, $M$ a bimodule. We define a bunch of spectra $U^n (R;M)$ with $C_n$ action by letting $U^n (R;M)$ be the derived cyclic tensor product (over $R$) of $n$ copies of $M$.

There is an evident $C_n$ action on $U^n (R;M)$ given by permuting the factors, and moreover when $n \mid N$, we have natural restriction maps between the fixed points

$$res : U^N (R;M)^{C_N} \rightarrow U^n (R;M)^{C_n}.$$

We then define

$$W(R;M) := holim_{res} U^n (R;M)^{C_n}.$$

Example. $U^1 (R;M) \simeq THH(R;M)$ as normally defined, and if $R = M$ then we have that $W(R;M) \simeq TR(R;M)$.

This functor $W(R;M)$ is meant to be an attempt to define $TR$ in the absence of the cyclic symmetry that is present when $M = R$. The remarkable thing is that this actually works! The nomenclature is justified by the following $p$-typical statement:

Theorem. (Hesselholt-Madsen) $\pi_0 (TR(R;p)) \simeq W_{(p)}(R),$

where the latter is a suitable version of $W(R;M)$ that takes a homotopy limit over only $U^{p^n}(R;M)^{C_{p^n}}$.

The virtue of this setup is that we have explicit understanding of what the layers of the Taylor tower of $W(R;-)$ look like, as well as various splitting theorems, e.g. we have the following ``fundamental cofibration sequence’’:

Theorem. There is a homotopy fiber sequence

$$U^n (R; M)_{hC_n} \rightarrow W^{n}(R; M) \rightarrow W^{(n-1)}(R; M),$$

where $W^{n}(R;M)$ are the functors obtained by truncating the homotopy limit defining $W(R;M)$.

Moreover, we have that $W^{n}(R;M)$ is the $n$th polynomial approximation of $W (R;M)$, so this is the fiber sequence that computes the layers of the Taylor tower.

Generalizations

The problem with the Lindenstrauss-McCarthy story is that it is only proven for discrete rings, but all of the constructions floating around can just as well be made when $R$ is a connective ring spectrum and $M$ is a (simplicial) $R$-bimodule.

One of the great tricks that one can do is to use the resolution of connective ring spectra by simplicial rings. That is, given a connective ring spectrum $R$, there is a $id$-Cartesian cube with initial vertex $R$, and such that all other vertices are canonically stably equivalent to the Eilenberg-MacLane spectrum of a simplicial ring.

The following fact lets us promote results about simplicial rings to those about connective ring spectra:

Theorem. If $\chi$ is an $(id)$-Cartesian $k$-cube of connective ring spectra, then the cube $K(\chi)$ is $(k+1)$-Cartesian.</span>

Idea for proving generalization: Show that the functors $W(-;-), \tilde{K}(-;-)$ have a similar property, so that the equivalence given by Lindenstrauss and McCarthy can be promoted to one for connective ring spectra.

This works just fine, and we arrive at:

Theorem. (P.) The Lindenstrauss-McCarthy result hnews for connective ring spectra.

Unfortunately, this is mostly just a one-off trick, and we are still looking for a good conceptual understanding of what the Lindenstrauss-McCarthy equivalence really means. It largely goes back to the Dundas-McCarthy theorem mentioned earlier, which can also be proven for connective ring spectra, but fails to admit a generalizable proof. The issue that arises there is that their proof relies heavily on the linear models of $K$-theory when working over discrete rings, and these simply faily to work when we move to other contexts (their proof involves the addition of maps, a simplicial model of $K$-theory, etc.).

If we had a good way of dealing with the coherence issues in defining the Dundas-McCarthy maps, then we might be able to generalize the proof and understand what’s going on, but that’s something that has yet to be done.

I heard an idea tossed around recently that I’d like to share with you all. I worry that it might be a little half-baked, as I’ve only heard about it recently and so maybe haven’t spent enough time sketching out the edges of it. Maybe writing this will help. Throughout, $k$ is a perfect field of positive characteristic $p$.

Where Lie theorists study Lie algebras, formal algebraic geometers study (covariant) Dieudonné modules. The essential observation is that the sorts of formal Lie groups appearing in algebraic topology are commutative and one-dimensional, meaning that their associated Lie algebras are one-dimensional vector spaces with vanishing brackets, and so it is unreasonable to think that it would carry much interesting information about its parent formal Lie group. To correct for this, one takes the collection of all curves on the formal group (i.e., without reducing to their linear equivalence classes, as one does when building the Lie algebra) and remembers enough structure stemming from the group multiplication that this assignment

$$D: \left\{\text{formal groups}\right\} \longrightarrow \left\{\begin{array}{c}\text{collections of}\;p\text{-typical curves} \\ + \\ \text{structure} \end{array}\right\}$$

becomes an equivalence. Such collections of curves form modules, called “Dieudonné modules”, over a certain ground ring, called the Cartier ring, which is built upon the ambient field $k$. The three relevant pieces of structure are the actions of homotheties, of the Frobenius, and of the Verschiebung, which were all described way back in this post on Witt vectors. (In the notation of that post, we’re interested just in $F_p$ and $V_p$.) Altogether, this gives a formula for the Cartier ring:

$$\mathrm{Cart}(k) = \mathbb{W}(k)\langle F,V \rangle / \left(\begin{array}{c}VF = FV = p, \\ Fa = a^\sigma F, \\ aV = Va^\sigma\end{array}\right).$$

Say that a Dieudonné module is formal when it is: finite rank; free as a $\mathbb{W}(k)$-module; reduced, meaning that it’s $V$-adically complete; and uniform, meaning that the natural map $M / VM \to V^k M / V^{k+1} M$ is an isomorphism. Then, the Dieudonné functor on finite height formal groups lands in the subcategory of formal Dieudonné modules, and there it restricts to an equivalence. Actually, more is true: the Dieudonné module of a $p$-divisible group can be made sense of, and Dieudonné modules which are free of finite rank (but without reducedness or uniformity) are equivalent to $p$-divisible groups.

Dieudonné modules are thrilling because they are just modules, whereas $p$-divisible groups are these unwieldy ind-systems of finite group schemes. The relative simplicity of the data of a Dieudonné module allows one to compute basic invariants very quickly:

Theorem: Take $\mathbb{G}$ to be a $p$-divisible group and $M$ its Dieudonné module. There is a natural isomorphism of $k$-vector spaces $T_0 \mathbb{G} \cong M / VM$. In the case that $\mathbb{G}$ is one-dimensional, then the rank of $M$ as a $\mathbb{W}(k)$-module agrees with the height $d$ of $\mathbb{G}$. Moreover, if $\gamma$ is a coordinate on $\mathbb{G}$ (considered as a curve), then $\{\gamma, V\gamma, \ldots, V^{d-1} \gamma\}$ forms a basis for $M$.

There is also something like a classification of the simple Dieudonné modules over $\bar{\mathbb{F}}_p$ (where, among other things, the étale component of a p-divisible group carries little data):

Theorem (Dieudonné): For $m$ and $n$ coprime and positive, set

$$G_{m,n} = \mathrm{Cart}(\bar{\mathbb{F}}_p) / (V^m = F^n).$$

Additionally, allow the pairs $(m, n) = (0, 1)$ to get

$$G_{0,1} = D(\mathbb{G}_m[p^\infty])$$

and $(m, n) = (1, 0)$ to get

$$G_{1,0} = D(\mathbb{Q} / \mathbb{Z}).$$

(All these modules $G_{m,n}$ have formal dimension $n$ and height $(m+n)$.) For any simple Dieudonné module $M$, there is an isogeny $M \to G_{m,n}$, i.e., a map with finite kernel and cokernel. Moreover, up to isogeny every Dieudonné module is the direct sum of simple objects.

Every abelian variety $A$ comes with a p-divisible group $A[p^\infty]$ arising from its system of $p$-power order torsion points. This connection is remarkably strong; for instance, there is the following theorem:

Theorem (Serre–Tate): Over a $p$-adic base, the infinitesimal deformation theories of an abelian variety $A$ and its $p$-divisible group $A[p^\infty]$ agree naturally.[1]

For this reason and others, the $p$-divisible group of an abelian variety carries fairly strong content about the parent variety. On the other hand, it is not immediately clear which $p$-divisible groups arise in this way. Toward this end, there is a symmetry condition:

Lemma (“Riemann–Manin symmetry condition”): As every abelian variety is isogenous to its Poincaré dual and the corresponding (Cartier) duality on $p$-divisible groups sends ($V$ to $F$ and hence) $G_{m,n}$ to $G_{n,m}$, these summands must appear in pairs in the isogeny type of the Dieudonné module of $A[p^\infty]$.

As a simple example, this gives the usual categorization of elliptic curves: an elliptic curve is $1$-dimensional, hence has $p$-divisible group of height $2$. One possibility, called a supersingular curve, is for the Dieudonné module to be isogenous to $G_{1,1}$; this is a $1$-dimensional formal group of height $2$ and it satisfies the symmetry condition. The only other possibility, called an ordinary curve, is for the Dieudonné module to be isogenous to $G_{1,0} \oplus G_{0,1}$; this is the sum of a $1$-dimensional formal group of height $1$ with an étale component of height $1$, and it too satisfies the symmetry condition.

A remarkable theorem is that the converse of the symmetry lemma hnews as well:

Theorem (Serre, Oort; conjectured by Manin): If a Dieudonné module $M$ satisfies the above symmetry condition, then there exists an abelian variety whose $p$-divisible group is isogenous to $M$.

Both proofs of this theorem are very constructive. Serre’s proof explicitly names abelian hypersurfaces whose $p$-divisible groups are of the form $G_{m,n} \oplus G_{n,m}$, for instance.

Now, finally, some input from algebraic topology. The Morava $K$-theories of Eilenberg–Mac Lane spaces give a collection of formal groups which can be interpreted in the following way:

Theorem (Ravenel–Wilson): For $1 < m \le n$, the $p$-divisible group associated to $K(n)^* K(\mathbb{Q}/\mathbb{Z}, m)$ is (in a suitable sense) the $m$th exterior power of the $p$-divisible group $K(n)^* K(\mathbb{Q}/\mathbb{Z}, 1)$. It is smooth, has formal dimension $\binom{n-1}{m-1}$, and has height $\binom{n}{m}$. (Additionally, it is zero for $m > n$.)

Theorem (Buchstaber–Lazarev): For $1 < m \le n$, the same $p$-divisible group has Dieudonné module isogenous to the product of $\frac{1}{n_0} \cdot \binom{n}{m}$ copies of $G_{n_0-m_0,m_0}$, where $m_0/n_0$ is the reduced fraction of $m/n$.

The conclusion of Buchstaber and Lazarev is that this means that these $p$-divisible groups almost never have realizations as abelian varieties, since they mostly don’t satisfy the symmetry condition. The only time that they do is something of an accident: when $n$ is even and $m = n/2$, then the corresponding Dieudonné module is isogenous to that of a large product of copies of a supersingular elliptic curve. However, Ravenel observed that Pascal’s triangle is symmetric:

Observation (I heard this from Ravenel, but surely Buchstaber and Lazarev knew of it): The sum of all of the Dieudonné modules

$$\bigoplus_{m=0}^{\text{$n$ (or $\infty$)}} D(\operatorname{Spf} K(n)^* K(\mathbb{Q}/\mathbb{Z}, m))$$

satisfies the Riemann-Manin symmetry condition.

This is an interesting observation. In light of the comments at the end of the Buchstaber–Lazarev paper, one wonders: why privilege $m = n/2$? But, even more honestly, why privilege $m = 1$ in our study of chromatic homotopy theory? A recurring obstacle to our understanding of higher-height cohomology theories has been the disconnection from the picture of globally defined abelian varieties. Could there be a naturally occurring abelian variety whose $p$-divisible group realizes the large ($2^{n-1}$-dimensional!) formal group associated to the $K$-theoretic Hopf ring of Eilenberg–Mac Lane spaces?

The explicit nature of the solutions to Manin’s conjecture show us that, yes, it is certainly possible to write down large products of hypersurfaces to give a positive answer to this question with the words “naturally occurring” deleted. This alone isn’t very helpful, however, and so to pin down what we might be even talking about there are a number of smaller observations that might help:

• If such an abelian variety existed, there would be a strange filtration imposed on its $p$-divisible group arising from the degrees of the Eilenberg–Mac Lane spaces. The Riemann–Manin symmetry condition tells us that these $G_{m,n}$ and $G_{n,m}$ factors must come in pairs, but in almost all situations, one pair appears on one side of the middle-dimension $n/2$ and the other appears on the other side. What could this mean in terms of the hypothetical abelian variety?
• Relatedly, this pairing arises from the “$\circ$-product” structure on the level of Hopf algebras, or as a sort of Hodge-star operation on the level of Dieudonné modules. What sort of structure on the abelian variety would induce such an operation, and in such an orderly fashion?
• There should be accessible examples of these hypothetical varieties at low heights. For instance, the one associated to height $1$ via mod-$p$ complex $K$-theory is (canonically, not merely isogenous to) a sum $G_{1,0} \oplus G_{0,1}$ — i.e., it comes from an ordinary elliptic curve. Can we identify which elliptic curve — and in what sense we can even ask this question? Is there a naturally occurring map from the forms of $\mathbb{G}_m$ to the ordinary locus on the (noncompactified?) moduli of elliptic curves? What about forms of $\hat{\mathbb{G}}_m$? What if we select a supersingular elliptic curve instead — is there an instructive assignment to abelian varieties whose Dieudonné module has isogeny type $G_{1,0} \oplus G_{1,1} \oplus G_{0,1}$? (On the face of it, this last bit doesn’t look so helpful, but maybe it is.)

[1] - Presumably this can be expressed by saying that the map from a moduli of abelian varieties to a moduli of $p$-divisible groups is formally étale, but no one seems to say this, so maybe I’m missing something.

---

I’ve been making an effort to learn some arithmetic geometry recently. I started with local class field theory, which was mind-blowing. When I was a first year, someone sat me down and instructed me that I must take a course in complex geometry to become competent — and they were right, and it was a wonderful course, and I’m really glad I got that advice. I have no idea how (especially as I’ve been bumbling about with formal groups for so long!) it slipped past me that local class field theory is another one of these core competencies, and really one of the great achievements of twentieth century mathematics.

I gave a kind of measly talk about this a month ago, when I was trying to stir up interest in a reading group. The notes are a little batty, but they’re fun enough, and you can find them here.

---

Speaking of mind-blowing things, last week there was a week-long workshop on perfectoid spaces at MSRI, which I attended between one-third and one-half of. There are video lectures available on the MSRI website; at the very least everyone should watch Scholze’s introduction, just to get a sense of what all the fuss is about, and then ideally both of Weinstein’s lectures, which were excellent and very much adjacent to the subject of this post — this blog, really.

And, as an uninspired parting remark, we topologists do have access to the pro-system

$$\left( \cdots \xrightarrow{p} \mathbb{C}\mathrm{P}^\infty \xrightarrow{p} \mathbb{C}\mathrm{P}^\infty \xrightarrow{p} \mathbb{C}\mathrm{P}^\infty\right) \ldots$$