Chromotopy

Reduced words

This past summer I helped out a bit on an REU project, on extending a few results and conjectures from this paper. Those results/conjectures are both amazing and easy to describe (if not to prove), so I want to do that here. It’s also a nice excuse to talk about the story of reduced words for permutations.

Let $s_i$ be the transposition $(i\, \,\,\,i+1)$. A reduced word for a permutation $w$ is a sequence $a = a_1 \cdots a_{\ell}$ of integers such that $w = s_{a_1} \cdots s_{a_{\ell}}$ and $\ell$ is minimal. That is, a reduced word is a minimal way of getting from $12\cdots n$ to $w$ by repeatedly interchanging adjacent entries.

Examples

There are 2 reduced words for $w = 2143$:

$$1234 \,\xrightarrow{1}\, 2134 \,\xrightarrow{3}\, 2143 \,\leadsto\, a = 13$$ $$1234 \,\xrightarrow{3}\, 1243 \,\xrightarrow{1}\, 2143 \,\leadsto\, a = 31$$

$w = 321$ has 2 also: $a = 121$ and $212$.

A little thought will show that the length of a reduced word for $w$ is the same as the length of $w$, the number of inversions in $w$: pairs $i < j$ such that $w_i > w_j$ . It’s also not hard to see that reduced words always exist, i.e. that the symmetric group is generated by adjacent transpositions.

The element of $S_n$ of greatest length is the reverse permutation $w_0 = n(n-1)\cdots 21$ , having length ${n \choose 2}$ . The basic question of Angel et al. is: what does a random reduced word for $w_0$ look like? We’ll look at two ways of visualizing a reduced word. First, think of a reduced word $a = a_1 \cdots a_{\ell}$ as a sequence of permutations:

$$1,\quad s_{a_1},\quad s_{a_1} s_{a_2},\quad \ldots,\quad s_{a_1} \cdots s_{a_\ell}.$$

For each entry $1, \ldots, n$, track its position in each permutation in the sequence. Since at each step we just switch two adjacent entries, positions change by at most 1 each time, so we can hope to get nice-looking piecewise curves. To be precise, for each $i$, draw the path which connects the points

$$(0, i), (1, s_{1}(i)), (2, s_{a_1} s_{a_2}(i)), \ldots.$$

Here’s what you get, for $n = 500$ (having drawn only some of the paths, to reduce clutter):

Are these… sine waves?

Let’s press on. Consider the same sequence of permutations

$$1,\quad s_{a_1},\quad s_{a_1} s_{a_2},\quad \ldots,\quad s_{a_1} \cdots s_{a_\ell}.$$

but now draw their graphs, as functions $\{1, \ldots, n\} \to \{1, \ldots, n\}$ , in sequence. In the following picture we do that and then go back to the identity.

 

!!!

Angel et al. don’t quite prove that you get these sine wave and rotating disk pictures in the limit, but they do give an attractive geometric interpretation of reduced words which should explain the pictures, in terms of the permutahedron. Instead of that, though, I’ll talk about how one samples reduced words uniformly at random to create these pictures. This might not sound so exciting, but in fact leads to some rather nice mathematics.

The obvious thing to do to choose a reduced word $a$ for $w$ is start with $12\cdots n$ , choose a random adjacent pair which isn’t an inversion, swap it, and repeat until you’re at $w$. Unfortunately, this doesn’t give a uniform distribution (try it for $w = 4321$). To understand how Angel et al. solve this problem, we’ll go back to the 80s when Stanley was thinking about counting reduced words. First, however, we need some basics about symmetric functions.

Symmetric functions

A symmetric function is a formal power series $f(x_1, x_2, \ldots)$ in infinitely many variables, with integer coefficients, which remains unchanged under permutation of the variables: if $\sigma \in S_n$ , then $f(x_{\sigma(1)}, x_{\sigma(2)}, \ldots) = f(x_1, x_2, \ldots)$ . [We should also assume $f$ has terms of only finitely many different degrees, so that the ring of symmetric functions is graded by degree]. For example:

$x_1 + x_2 + x_3 + \cdots$  or  $x_1 x_2 + x_1 x_3 + x_2 x_3 + \cdots\,;$

more generally, the elementary symmetric function $e_k = \sum_{1 \leq i_1 < \cdots < i_k} x_{i_1} \cdots x_{i_k}$ , the sum of all squarefree degree $k$ monomials.

Here’s one reason to care about symmetric functions: they’re characters of $GL_n$-modules. Suppose $E$ is a finite-dimensional complex $GL_n(\mathbb{C})$-module, and let $T$ be the subgroup of diagonal matrices in $GL_n$ . To avoid awful things let’s assume $E$ is really a representation of $GL_n$ as an algebraic group, meaning that the defining map $\rho : GL_n \to GL(E)$ is a map of varieties. Given $X \in T$ with diagonal entries $x_1, \ldots, x_n$ , the character of $E$ is $\chi_E(x_1, \ldots, x_n) = \text{tr} \rho(X)$ . Basic representation theory (Schur’s lemma) shows this is a symmetric (Laurent^1) polynomial in $x_1, \ldots, x_n$ .

For example, take $E = \bigwedge^k \mathbb{C}^n$ , and a basis $e_1, \dots, e_n$ of $\mathbb{C}^n$ . Any basis vector $e_{i_1} \wedge \cdots \wedge e_{i_k}$ for $E$ is an eigenvector for $X$ , with eigenvalue $x_{i_1} \cdots x_{i_k}$ . Now $\chi_E$ is the sum of all these eigenvalues, which is just the elementary symmetric function $e_k(x_1, \ldots, x_n)$ . It’s similarly easy to see that the character of $Sym^k \mathbb{C}^n$ is the homogeneous symmetric function

$$h_k = \sum_{1 \leq i_1 \leq \cdots \leq i_k \leq n} x_{i_1} \cdots x_{i_k}.$$

[The fact that we now just have finitely many variables can be safely glossed over.]

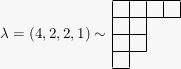
From this point of view, there are some obvious symmetric functions to look at: the characters of simple $GL_n$-modules. These turn out to be naturally indexed by partitions — finite integer sequences $\lambda = (\lambda_1 \geq \cdots \geq \lambda_{\ell})$, where $\ell \leq n$ . Say $\lambda$ is a partition of $n$ if $\mid \lambda \mid = \sum_i \lambda_i = n$. The Ferrers diagram of a partition $\lambda$ is gotten by drawing a left-justified row of $\lambda_i$ boxes for each $i$ , starting at the top and going down:

 

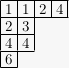
A semistandard tableau (plural tableaux) of shape $\lambda$ is a filling of the boxes of the Ferrers diagram of $\lambda$ with positive integers which is strictly increasing down columns, weakly increasing rightward across rows:

To a semistandard tableau $T$, associate a monomial $x^T = \prod_{i \in T} x_i$, the product of $x_i$ as $i$ ranges over the entries of the tableau. For the tableau above, this monomial is $x_1^2 x_2^2 x_3 x_4^3 x_6$. Now given a partition $\lambda$, the Schur function $s_{\lambda}$ is

$$s_{\lambda} = \sum_T x^T,$$

where $T$ ranges over all semistandard tableaux of shape $\lambda$. It’s less than obvious from this definition that $s_{\lambda}$ is symmetric, but it is. The Schur functions $s_{\lambda}(x_1, \ldots, x_n)$ as $\lambda$ runs over partitions with length at most $n$ turn out to be (almost^1) exactly the irreducible characters of $GL_n$.

Examples

If $\lambda = (k)$, a semistandard tableau of shape $\lambda$ is a weakly increasing sequence $1 \leq i_1 \leq \cdots \leq i_k$. The Schur function $s_{(k)}$ is $h_{(k)}$ above, associated to $\text{Sym}^k \mathbb{C}^n$.

If $\lambda = (1, \ldots, 1) = (1^k)$, a semistandard tableau of shape $\lambda$ is a strictly increasing sequence $1 \leq i_1 < \cdots < i_k$, and $s_{(1^k)} = e_k$, associated to $\bigwedge^k \mathbb{C}^n$.

If $\lambda = (2,1)$, there are 2 semistandard tableaux with entries at most 2,

$$\begin{array}{cc} 1 & 1\\ 2 & \, \end{array}\quad \begin{array}{cc} 1 & 2\\ 2 & \, \end{array},$$

and so $s_{(2,1)}(x_1, x_2) = x_1^2 x_2 + x_1 x_2^2$. To locate the corresponding $GL_2(\mathbb{C})$ module, do a bit of algebra:

$$s_{(2,1)}(x_1, x_2) = (x_1 + x_2)(x_1 x_2) = h_1 e_2,$$

so the module should be $\mathbb{C}^2 \otimes \bigwedge^2 \mathbb{C}^2$.

One last fact that we’ll need, which follows from the realization of Schur functions as irreducible characters: as $\lambda$ ranges over all partitions of $n$, the Schur functions $s_{\lambda}$ form a $\mathbb{Z}$-basis of the degree $n$ symmetric functions.

Stanley symmetric functions

Let’s get back to reduced words. If $\lambda$ is a partition of $n$, meaning that $\mid \lambda \mid = \sum_i \lambda_i = n$, a standard tableau of shape $\lambda$ is a semistandard tableau of shape $\lambda$ with entries $1, \ldots, n$. For example, $(2,1)$ has two standard tableaux,

$$\begin{array}{cc} 1 & 2\\ 3 \end{array}, \quad \begin{array}{cc} 1 & 3\\ 2 \end{array}.$$

Stanley noticed the following coincidence: for $1 \leq n \leq 6$, the number of reduced words for $n(n-1)\cdots 21$ matches the number of standard tableaux of the staircase shape $\delta_n = (n-1, n-2, \ldots, 1)$; we’ve seen this for $n = 3$. The numbers are 1, 1, 2, 16, 768, 292864, so this is pretty convincing.

Now we define a somewhat mysterious-looking symmetric function. The Stanley symmetric function of a permutation $w$ is

$$F_w = \sum_{a \in \text{Red}(w)} \sum_{i \in C(a)} x_{i_1} \cdots x_{i_\ell},$$

where $\text{Red}(w)$ is the set of reduced words of $w$, and $C(a)$ is the set of integer sequences $1 \leq i_1 \leq \cdots \leq i_\ell$ such that if $a_j &gt; {j+1}$, then $i_j < i_{j+1}$. Here $\ell$ is the length of $w$.

[Where does this come from? It seems plausible that Stanley was aiming for $F_{w_0} = s_{\delta_n}$, for reasons which will become clear below, and already knew about similar “quasisymmetric” expansions for Schur functions.]

Example

Take $w = 2143$, with reduced words $31, 13$. Then $C(13) = \{1 \leq i \leq j\}$ and $C(31) = \{1 \leq i < j\}$, so

$$F_{2143} = h_2 + e_2 = s_{(2)} + s_{(1,1)}.$$

In this example $F_w$ is visibly symmetric, which is true in general, if not at all obvious.

 

Here’s the key enumerative fact. Right from the definitions we see that the coefficient of $x_1 \cdots x_n$ in $s_{\lambda}$ is the number of standard tableaux of shape $\lambda$; call it $f^{\lambda}$. On the other hand, $12\cdots \ell \in C(a)$ for any reduced word $a$, and so the coefficient of $x_1 \cdots x_\ell$ in $F_w$ is the number of reduced words of $w$. So, if we write

$$F_w = \sum_{\lambda} a_{\lambda} s_{\lambda},$$

then $\mid \text{Red}(w) \mid = \sum_{\lambda} a_{\lambda} f^{\lambda}\,$!

Of course this isn’t so useful without a reasonable way of getting at the Schur decomposition of $F_w$. This post is long enough, so next time I’ll describe three such ways: one combinatorial (which will also solve the problem of sampling from $\text{Red}(w_0)$ uniformly), one representation-theoretic (since $F_w$ is a symmetric function, maybe it’s the character of some module???), and one based on the geometry of Schubert varieties.

Notes

¹ Here “Laurent” and “almost” have the same explanation: the 1-dimensional representations of $GL_n$ where $A$ acts as multiplication by $\det(A)^{-k}$ for some positive integer $k$.

A Serif blog | View archive of 36 posts